Арифметика Магницкого - зеркало средневековья.
При расшифровке текстов Нострадамуса современным исследователям приходится так или иначе учитывать те знания, которые были, а вернее могли быть, у людей в XVI веке. Нашему предсказателю приписывают гениальные, и даже фантастические научные знания и способности. Но соответствует ли это реальному состоянию научной мысли в те времена? На каком уровне знаний была наука средневековья? Какими методами и приёмами пользовались те же математики или астрологи в XVI веке, - во времена Мишеля Нострадамуса? Ответив на эти вопросы, у нас появится шанс яснее понять, что мог и чего не мог Нострадамус и какого типа шифр он мог применить в своих посланиях.
Китайская ложь и русские свидетельства.
Недавно, заглянув в википедию, я был поражён информацией о том, что теорему Пифагора придумали и доказали китайцы! Я давно заметил, что наши узкоглазые "друзя" в течение XX века пытались переписать всю историю человечества под себя. Они и порох изобрели, хотя ни в Китае, ни в ближайших к нему странах нет, и никогда не было месторождений селитры - составной и незаменимой части пороха. Они и великие путешественники, но в других странах их пребывание ни в древности, ни в средние века не зафиксировано. Они и великие мореплаватели и даже плавали через Индийский океан до Африки и обратно тысячу лет назад, но современные не китайские инженеры, произведя расчёты, вынесли неутешительный и окончательный вердикт: корабли такой конструкции, какая указана в якобы древних чертежах, построить невозможно. Они и фарфор первые придумали, однако древние китайские изделия до неприличия напоминают русский фарфор фирмы Гжель. Для примера, в таблице ниже, приведены фотографии русских и китайских фарфоровых изделий. Попробуйте, уважаемые читатели, сами сказать, где китайская и где наша посуда. А я дам ответ в конце статьи.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Как известно, начало производства русского фарфора в г. Гжель теряется во тьме веков. Уже в XV веке, при Иване Грозном, это производство считалось очень древним и широко известным. Но наших китайских соседей это не смущает. Если так дальше пойдёт, то скоро они и Пифагора объявят китайским мандарином.
Особо хочу упомянуть про «Великий шелковый путь». Этот термин вошел в историческую науку в конце XIX века, после публикации в 1877 немецким историком К. Рихтгофеном книги Китай. То ли этот историк придумал данное словосочетание, то ли ему подсказали сами китайцы, но с тех пор мы узнали, что наши предки, оказывается, только и делали, что шастали в Китай. Но только почему-то туда ничего не везли. Видимо европейские товары были в Китае без надобности. А оттуда привозили только шёлк, который, почему-то, китайским никто не называл.
В существование такого сверхдлинного торгового пути ещё как-то можно было бы поверить, но только у нас имеется более древнее "железобетонное" свидетельство Афанасия Никитина. В своих записках "Хожение за три моря" во время путешествия по территории Индии он свидетельствует:
В Бидаре (город в Индии) на торгу продают коней, камку, шелк и всякий иной товар да рабов черных, а другого товара тут нет. Товар всё гундустанский (индостанский, т. е. индийский), а из съестного только овощи, а для Русской земли товара нет.
В Индии нет товара для Руси? Как же так? Почему шёлк не заинтересовал русского купца Афанасия? Может на Руси имел хождение шёлк из Китая? Тогда вот она - золотая жила. Зачем ездить в Китай, если такой же товар можно купить в Индии? Если посмотрим на карту, то увидим, что Индия в полтора-два раза ближе к Волге, чем Китай. К тому же при путешествии в Китай приходится пересекать страшную пустыню Гоби. Следовательно, возить шёлк из Индии гораздо быстрее, удобнее и выгоднее, чем из далёкого Китая. Но почему-то русские купцы этой новости не обрадовались.
Здесь нужно отметить, что Афанасий Никитин в этом тексте даёт нам ещё одно важное свидетельство - то, что шёлк в Индии был свой, а не китайский (Товар всё гундустанский). Но тогда откуда он там взялся? А он там всегда был. И не только там. Дело в том, что ареал распространения тутового шелкопряда занимает огромную территорию от Китая до Средиземного моря. И если шёлк в качестве товара для русских людей был не интересен, то это могло быть только в том случае, если на Руси своего шёлка девать было некуда. Не нужно забывать, что климат в те времена был другой и, например, на Соловках выращивали виноград.
К чему я всё это говорю? Да к тому, что искажением исторической памяти занимались очень многие и довольно часто. Поэтому рассмотрение какой-либо исторической эпохи - это как хождение по минному полю - того и гляди, что наткнёшься на ложь, фальсификацию, подтасовку фактов или просто буйную фантазию очередного экзальтированного историка. А чтобы не ошибиться, нужно основывать свои знания не на мнении авторитетов, а на исторических документах. Вот один из таких документов я и предлагаю рассмотреть.
АРИФМЕТИКА.
В 1703 году по приказу Петра I в Москве был напечатан учебник математики под названием "Арифметика". Автором её был Леонтий Филиппович Магницкий (1669-1739 г.г.). Его учебник стал величайшим научно-прикладным произведением Российской империи. В ней были собраны не только все достижения математической науки того времени, но и много новых элементов. Например, впервые в мировой истории приведены такие понятия, как произведение, множитель, делитель, возведение в квадрат, извлечение квадратного корня и т. д.
 |
| стр. 46 |
Этот учебник был настолько удачным и оригинальным, что выдержал множество переизданий. Полтора столетия (до середины XIX в.) он был почти единственным учебником по математике для всех слоёв населения. По нему учились и Ломоносов, и Пушкин, и Лермонтов.
В Интернете можно найти много хвалёных отзывов о содержимом этого учебника, но я хочу заострить внимание читателей на том, чего в нём нет. А нет в нём очень многого:
1) нет ни теорем, ни их описаний;
2) нет доказательств этих теорем или чего-либо;
3) нет упоминаний античных математиков (Архимеда, Пифагора и др.).
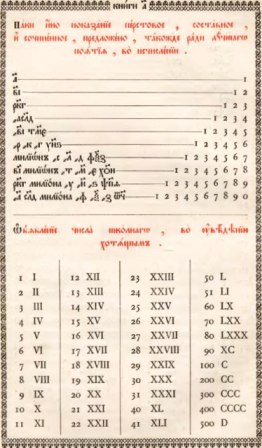
Даже цифры, знаменитые римские цифры никак не обозначены. На странице 46 (см. фото) Магницкий знакомит читателей-учеников с римскими цифрами и приводит таблицу, в которой показано как арабские цифры соответствуют римским. Следует особо отметить, что это мы сейчас их так называем, но у Магницкого арабские цифры почему-то названы "школьные", а у римских вообще нет названия. Казалось бы, в те времена люди ещё должны были помнить, откуда что взялось. Но нет. Ни на этой странице, ни во всём учебнике, нет даже намёка на иностранное происхождение любых цифр. Это в некоторой степени подтверждает теорию, высказанную мной в статье "Арабские цифры - русские цифры".
Да, раньше у римских цифр не было названия - это были обычные "черты и резы". Они были обычным инструментом, давно используемым в быту. Поэтому усовершенствовать их, как говориться, сам бог велел. И это было сделано в XVII веке. Во времена Нострадамуса - в XVI веке, а значит и в более ранние времена, четвёрку обозначали как IIII. Именно такое обозначение римской цифры в нумерации центурий и катренов мы видим повсеместно в первых изданиях "Пророчеств Мишеля Нострадамуса". И только в издании 1649 года появляется современное обозначение четвёрки - IV.
Также и в "Арифметике" Магницкого на странице 46 мы видим уже современное начертание римских цифр.
Теорема Пифагора.
Да, действительно, вобрав в себя все основные достижения математической мысли того времени, в учебнике почему-то полностью отсутствуют фундаментальные основы для геометрических вычислений. Но задачки на тему теоремы Пифагора имеются. И не одна, а целых три.
 |
Примеры, применяемые в быту,
через извлечение квадратного корня творимые.
Случилось некоему человеку к стене лестницу приставить, стены же той высота была 117 стоп. И лестница была длиной 125 стоп. И узнать нужно на сколько стоп нижний конец этой лестницы нужно отодвинуть от стены (чтобы вершины совпали?); получится 44 стопы. А решать нужно так: возведи прежде высоту стены в квадрат, так 117 на 117 и получится 13689. Потом умножь длину лестницы так 125 на 125 и получится 15625, из него вычти квадрат стены 13689, и оставшееся 1936, раздели квадратным извлечением, и получится 44 как выше сказано, смотри здесь:
---------------------------------------------------------------------------------
дальше следуют вычисления в столбик (см. фото).
стр. 433 |
 |
Также ещё лестница к стене башни приставлена, её нижний конец отставлен от стены на 60 стоп, а высота стены 91 стопа. Узнай сколько стоп имеет длина лестницы: получится 109 стоп. А делать так: умножь прежде высоту стены квадратно (возведи в квадрат), расстояние до нижнего конца (лестницы) также квадратно умножи, и с квадратным произведением сложи, и из этой суммы квадратный корень извлеки, и получишь искомое, так как здесь:
---------------------------------------------------------------------------------
дальше следуют вычисления в столбик (см. фото).
стр. 434 |
 |
Также ещё лестница к башне приставлена, её длина 65 стоп, нижнего же конца отстояние от стены 16 стоп. И узнать нужно какую высоту имеет та стена; получится 63 стопы. А изобретай также, два данных размера, лестницы и отстояния от стены возведи в квадрат, и меньшее произведение вычти из большего, и из оставшегося извлеки квадратный корень, и будет искомая высота стены; смотри также следующее:
---------------------------------------------------------------------------------
дальше следуют вычисления в столбик (см. фото).
стр. 435 |
Эти три страницы из "Арифметики" Магницкого сами по себе очень показательны. Мы видим, что здесь нет устоявшихся терминов - автор в разных случаях применяет разные термины одних и тех же элементов, а такие элементы как катет, гипотенуза, прямой угол - вообще отсутствуют. Он ни разу не упоминает, ни Пифагора, ни его теорему. Он даже не объясняет, почему эти задачи нужно решать именно так, а не иначе. И почему именно эти задачи нужно решать таким методом? Есть задача, и есть её решение. Всё. Точка. И его за такое бедное описание задачи и её решения никто не осуждал!
Подобный подход к написанию учебника по математике можно объяснить только тем, что Магницкий не знал, ни теоремы Пифагора, ни каких либо других теорем. И никто не знал. В те времена никаких теорем ещё не существовало. Никому даже в голову не приходило что-либо доказывать. Самого принципа математических доказательств не было.
Кто-то может возразить, что подобное незнание Магницким древнегреческих, древнеримских и других мифов и первоисточников было только в немытой лапотной России, а вот в Европе, где уже давно существовали и академии, и университеты, вот там древних геометров и их теоремы давно знали и изучали. Но это не так. Ведь именно из-за полного отсутствия европейских учебников Пётр приказал Магницкому написать на русском языке, а не перевести с какого-нибудь другого языка, сей труд. Да, в Европе были университеты, но учили в них преимущественно слово божие. Как? Наизусть.
К области «науки» европейцы относили магию, алхимию, астрологию, демонологию. Впрочем, о какой образованности можно вести речь, если в 1600 г. в Риме сожгли Джордано Бруно, в 1616 г. запретили труд Коперника «Об обращении небесных тел», в 1633 г. Галилея заставили отречься от доказательств вращения Земли. Аналогичным образом в Женеве сожгли основоположника теории кровообращения Мигеля Сервета. Везалия за труд «О строении человеческого тела» уморили голодом в тюрьме.
Валерий Шамбаров.
А сказку о Пифагоре придумали видимо позже - в XVIII или XIX веке, после создания и доказательства самой теоремы.
Нужно заметить, что в античные времена решить любую теорему было в принципе невозможно, так как римскими цифрами невозможно произвести никаких математических операций, тем более в столбик. Поэтому в своей "Арифметике" Магницкий отвёл арабским цифрам четыре арифметических действия, а римским цифрам только одно пятое арифметическое действие - нумерацию. На большее римские цифры не годятся.
Калькуляторы и арифмометры.
Косвенным подтверждением моих выводов (далеко не оригинальных) служит странный всплеск изобретательской активности математиков именно с XVII века. Один за другим изобретаются и строятся машинки для счёта - арифмометры.
Ни в XVI-м, ни в более ранних веках не было сделано ни одного приспособления для счёта. Нет спроса - нет предложения. Но в начале XVII века, в 1631 г. У. Оутред вводит в научный обиход операцию "умножение" и присваивает ей условное обозначение (х), а в 1633 г. У. Джонс то же самое делает с операцией "деление" (:). Вероятно, что если в XVII веке были придуманы математические операции умножения и деления, а в столбик этого ещё не научились делать, то сразу появилась потребность в механических помощниках.
| Год создания |
Изобретатель |
Что сделано |
| 1623 г. |
Шиккард |
«вычислительные часы» |
| 1642 г. |
Паскаль |
«паскалина» |
| 1672 г. |
Лейбниц |
калькулятор |
| 1674 г. |
Морленд |
арифмометр |
Однако, в следующем - XVIII веке не было придумано ни одного арифмометра или калькулятора. Можно смело предположить, что такой длительный - более чем столетний - перерыв в изобретательской активности был обязан выходу в свет "Арифметики" Магницкого. Именно в ней были представлены для использования народными массами простые методы сложных арифметических расчётов. Например, люди научились вычислять в столбик. Поэтому, даже возведение любого числа в квадрат у них перестало вызывать затруднения. Машинки стали без надобности и изобретательство приостановилось. И только в 1820 г. Тома де Кольмар начал серийный выпуск арифмометров. Более подробно с математикой средневековья можно ознакомиться в документальном фильме "Плюс минус ноль. Арифметические загадки цивилизации". Его можно и посмотреть и скачать.
Арифметические фантазёры.
Напомню уважаемым читателям, что Мишель Нострадамус жил в XVI веке - с 1503 до 1566 г. Поэтому вопрос о математических способностях нашего лекаря сильно преувеличен. И подтверждением этому служит тот факт, что у Нострадамуса нет ни одного математического произведения. Да, сложение и вычитание в те времена уже были известны: знаки сложения (+) и вычитания (–) ввел Я. Видман в 1489 г. Но ни в одной своей книге или письме Нострадамус не упоминает ни одного математического действия, термина или формулы. И только в завещании приводятся "суммы подсчитанных денег". Но говорить о чём-то более серьёзном не приходится. Подумать только, какими выдающимися талантами и гениальными способностями должен был обладать наш Нострадамус, чтобы сварганить вот это убожество:
Эту пустышку он нарисовал в письме каноникам Оранжа, которое написал в конце своей жизни, но почему-то не отправил.
Однако, не смотря на более чем скромные познания Нострадамуса не то что в алгебре или геометрии, но даже в арифметике, многие современные энтузиасты пытаются найти какую-то суперформулу для расшифровки текстов пророка. Каждый в силу своих способностей и воображения пытается так переставить многочисленные числа в пророчествах Нострадамуса, чтобы получилось ну хоть какое-нибудь, ну хоть маленькое предсказание будущих событий. При этом используется такой бедный математический аппарат, такие посредственные математические способности, что становится стыдно за современное школьное образование. Глядя на жалкие потуги гореисследователей, так и хочется сказать: "такой арифметический штурм нам не нужен".
Чтобы показать, каких вершин можно достичь в деле пустого жонглирования цифрами предлагаю вашему вниманию статью из журнала "Наука и жизнь" за 1975 г. Сорок лет назад у этого журнала была традиция предлагать читателям решить или самим составить математические задачи, посвященные числу очередного года, в данном случае - 1975 году. Прочитав эту статью, пусть каждый исследователь пророчеств Мишеля Нострадамуса, каждый расшифровщик или очередной интерпретатор ещё раз крепко подумает, прежде чем решится опубликовать свой жалкий опус.
P.S.
В начале статьи на чётных фотографиях показаны русские фарфоровые изделия Гжель, а на нечётных - китайские.
Telecar.
13 января 2015 г.
|



