Журнал «Наука и жизнь» № 3, 1976 г., стр. 154-156.
МАТЕМАТИЧЕСКИЕ НЕОЖИДАННОСТИ

Год 1975.

С конца 1974 года в редакцию стали поступать письма с задачами, посвященными числу 1975. Папка с темой «Год 1975» постоянно пополнялась. Однако писем было меньше, чем в прошлом году. Наши корреспонденты то и дело жаловались на неудобство числа 1975. «Тяжелый год, вернее, тяжелое число 1975. Очень трудно с ним работать. Вот со следующим числом 1976 иметь дело любителям математики будет куда более приятно», - пишет А. Н. Сергеев из г. Томска. Но, несмотря на все сетования и затруднения, общие результаты конкурса (который, как и в прежние годы, получился стихийным) оказались очень неплохие.

* * *

Итак, сначала подведем итоги конкурса традиционных задач.

Первая конкурсная задача — изобразить число 1975 минимальным количеством одинаковых цифр с использованием математических знаков плюс, минус, умножение, деление квадратный корень, факториал. Разрешается использовать цифры как показатели степени и пользоваться скобками. В этом конкурсе победа присуждается читателям, затратившим минимальное количество цифр на представление «полного комплекта», то есть изображение числа 1975 с помощью одних единиц, одних двоек и т. д. Приводим лучшие решения первой задачи.
 

На «полный комплект» необходимо 69 цифр. Именно столько потребовалось для решения этой конкурсной задачи А. Л. Кабризону (г. Дрогобыч, Львовской области) и Н. И. Нестеренко (с. Лесная Поляна, Ворошиловградской области). В. А. Коржов (г. Минск) и В. Ф. Куров (Кировская область) для решения задачи использовали 70 цифр.

* * *

Вторая традиционная конкурсная задача: представить числа натурального ряда от 1 до максимально возможного с помощью цифр 1, 9, 7, 5, (не меняя их последовательности, пользуясь теми же математическими знаками, что и в первой конкурсной задаче). Приводим изображение нескольких первых чисел:
 

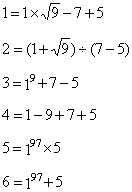и так далее
 

В этой задаче первым числом, которое никому не удалось представить с помощью заданных цифр, было число 53. Не смогли читатели справится и с числами 62, 63, 86, 87, 88, 90, 139, 147, 149. Для остальных чисел, до 151 включительно, были найдены соответствующие решения.

Лучших результатов в данном конкурсе достигли: А. Л. Кабризон, Н. И. Нестеренко и Ф. П. Степанов (Ворошиловградская обл.). На одно число (не получалось число 150) от них отстал В. А. Коржов.

* * *

Третья конкурсная задача. Изобразить число 1975 с помощью последовательностей цифр

используя минимальное число математических знаков. Сюда же примыкает задача - изобразить число 1975 с помощью последовательностей

Решения этих задач для числа 1975 получились достаточно компактными:
 

Авторы примеров В. Ф. Куров (2, 3, 4); В. А. Коржов (5, 6); Н. И. Нестеренко (1); А. Л. Кабризон (4); В. В. Безруков (г. Севастополь) (1) и целый ряд других читателей.

* * *

Несколько примеров решения еще одной традиционной задачи — изобразить число 1975 комплектом чисел 1, 9, 7, 5, 1, 9, 7, 5 с помощью математических знаков (без изменения порядка следования цифр).
 

Примеры составили: Г. Г. Грачев (1, 2), В. Ф. Куров (3).

* * *

Раздел фантазий конкурса «Год 1975».

Здесь вы найдете примеры и задачи, не ограниченные какими-либо условиями. Раздел открывает изображение числа 1975 В. Ф. Куровым:
 

* * *

Представляем задачу, которую прислал читатель Ф. П. Степанов (г. Перевальск, Ворошиловградской обл.).

Имеется n листов бумаги. Некоторые из них разрезаются на n частей. Получившиеся части, в свою очередь, тоже могут быть разрезаны на n частей и т. д. При каких значениях n можно ожидать, что после нескольких описанных операций общее число получившихся листков окажется равным 1975?

Следующие представления числа 1975 принадлежат тому же автору
 

* * *

Неплохо выглядят найденные Н. И. Нестеренко равенства
 

К наиболее удачным находкам автора можно, пожалуй, отнести следующие полиномы:
 

Полиномы интересны тем, что при х = 1, 2, 3, 4 полином А принимает значения 1, 9, 7, 5, а полином Б принимает значения .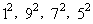

* * *

Ряд читателей представили число 1975 в виде прогрессий или выражений, включающих прогрессии:
 

В завершение приводим пример, про который В. А. Коржов пишет: «Особенно понравился мне в подборке «Год 1974» пример изображения числа 1974, принцип построения которого будет справедлив еще для целого ряда лет». Вполне естественно, что он  верен и для числа 1975:

* * *

Из 23 примеров и задач, присланных В. А. Коржовым, наиболее интересными нам показались следующие. Рассмотрим полином

* * *

* * *

Задача. Найти наименьшее положительное число, которое, будучи сложенным с любыми тремя числами из четырех: 1, 9, 7, 5, делится на оставшееся число.

* * *

* * *

Цифры числа 1975 удовлетворяют условию
 

Найти число, отличное от 1975 и удовлетворяющее тому же условию.

* * *

Два несложных примера на восстановление цифр:
 

* * *

Л. И. Николаев (г. Новгород) составил по аналогии с примером Ф. П. Степанова («Наука и жизнь» № 12, стр. 69) пирамиду для числа .
 

= 145598274390764 + 45598274390764 + 5598274390764 + ... + 764 + 64 + 4

и предлагает читателям составить такие пирамиды для чисел
 

Р. Я. Абакумов (г. Киев), В. Н. Шохленков (г. Гомель) и другие читатели заметили, что возможно составить магический квадрат 5X5 клеток с суммой 1975. Заполните квадратную таблицу последовательными положительными числами так, чтобы сумма на любой горизонтали, вертикали и каждой из главных диагоналей равнялась бы 1975.

Этой задачей мы и заканчиваем тему «Год 1975».

Наиболее успешно и активно в разработке темы «Год 1975» участвовали:

Н. И. Нестеренко (с. Лесная Поляна, Ворошиловградской области);

А. Л. Кабризон (г. Дрогобыч, Львовской области);

В. А. Коржов (г. Минск);

В. Ф. Куров (г. Слободской, Кировской области);

Г. Г. Грачев (с. Большие Березники, Мордовской АССР).